Import libraries.

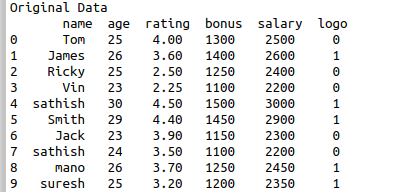
  Read the sample data.

  Define X and y variables.

  Build the logistic regression model.

  Split the sample data into training and test data.

  Fit the training data into the regression model.

#import libraries

import statsmodels.api as sm
import pandas as pd
from sklearn.model_selection import train_test_split

#read the data set

data=pd.read_csv(‘/home/soft27/soft27/Sathish/
Pythonfiles/Employee.csv’)

#creating data frame
df=pd.DataFrame(data)
print(df)

#assigning the independent variable
X = df[[‘rating’,’bonus’]]

#assigning the dependent variable
y = df[‘logo’]

#split data in training and test data
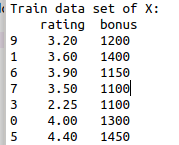
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
print(“Train data set of X:\n”,X_train)
print(“Train data set of y:\n”,y_train)

#build the model
model = sm.Logit(y_train, X_train)

#fit the model
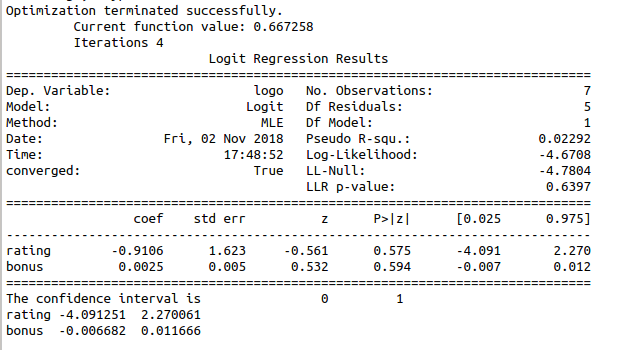
result = model.fit()

#take summary of model
print(result.summary())

#print the confidence interval
print(“The confidence interval is”,result.conf_int())