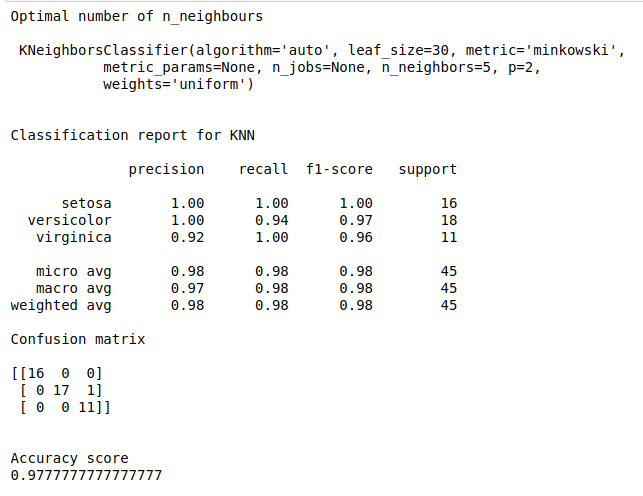
To find best fit n_neighbours in knn algorithm to improve performance of the model.
Iris data set
Improved classification results.
Import the library.
Load the sample data set..
Split the data train and test.
Define the number of n_neighbours.
Fit the train data into Gridsearch model.
Find the optimal number of n_neighbours.
Improve the model performance.
Calculate precision, recall and accuracy.
#import libraries
import warnings
warnings.filterwarnings(“ignore”)
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
#load the sample data from iris.csv file
data = pd.read_csv(‘/home/soft50/soft50/Sathish/practice/iris.csv’)
#Make it as a data frame
df = pd.DataFrame(data)
#feature variables
X = df.iloc[:,0:4]
y = df.iloc[:,4]
#Split the data into train and testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
#Knn
knn = KNeighborsClassifier()
#create a dictionary of all values we want to test for n_neighbors
params_knn = {‘n_neighbors’: np.arange(1, 25)}
#use gridsearch to test all values for n_neighbors
knn_gs = GridSearchCV(knn, params_knn, cv=5)
#fit model to training data
knn_gs.fit(X_train, y_train)
knn_best = knn_gs.best_estimator_
print(“Optimal number of n_neighbours\n\n”,knn_best)
y_pred = knn_best.predict(X_test)
#Evaluate the model
print(“\n”)
print(“Classification report for KNN\n”)
print(classification_report(y_test, y_pred))
print(“Confusion matrix\n”)
print(confusion_matrix(y_test, y_pred))
print(“\n”)
print(“Accuracy score”)
print(accuracy_score(y_test, y_pred))