To build simple linear regression model for train data in python.
Import necessary libraries.
Load the sample data set.
Assign the independent(X)and dependent(y) variables.
Pass the variables to the model.
Check normality of variable.
Test the correlation.
Build the linear model from sklearn library.
import pandas as pd
import scipy
from scipy import stats
#import correlation test method
from sklearn.linear_model import LinearRegression
#Load the sample data
data={‘salary’:[100,200,300,
400,500,400,300,200,100,50],
‘age’:[25,26,25,23,30,29,23,23,25,25],
‘rating’:[4,3.24,2.5,2.25,2,
2.25,2.5,2.75,3.2,4.2],’bonus’:[2500,
1200,900,3000,1800,1400,850,250,750,1000]}
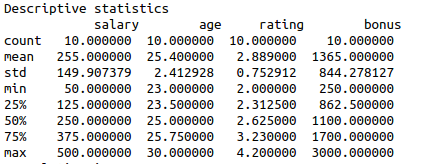
#Measuring descriptive statistics
df=pd.DataFrame(data)
print(“Descriptive statistics\n”,df.describe())
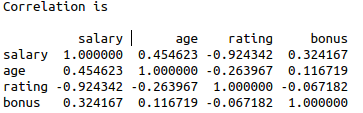
#Correlation
print(“Correlation is\n”)
print(df.corr(method=’pearson’))
#Take independent variable
X = df.iloc[:, :1].values
print(“Value of X is\n:”,X)
#Take dependent variable
y = df.iloc[:, 3].values
print(“Value of y is:\n”,y)
#building linear model
regressor = LinearRegression()
#Fit the variable to the linear model
t=regressor.fit(X, y)
#print the results
print(“Regression intercept is”,regressor.intercept_)
print(“Regression coefficient is”,regressor.coef_)