Amazing technological breakthrough possible @S-Logix pro@slogix.in

Office Address

  • #5, First Floor, 4th Street Dr. Subbarayan Nagar Kodambakkam, Chennai-600 024 Landmark : Samiyar Madam
  • pro@slogix.in
  • +91- 81240 01111

Social List

How to find Eigenvalues and Eigen vectors of an array using scipy

Description

To find Eigenvalues and Eigen vectors of an array using python scipy.

Input :

2D array.

Output:

Eigenvalues and Vectors.

Process

  Import Linear algebra from scipy.

  Define a simple 2D array.

  Pass it to the linalg.eig().

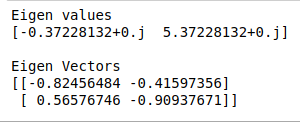
  Print the Eigenvalues and Eigen vectors.

Sample Code

from scipy import linalg
import numpy as np

#define a 2-dimensional array
sample_array = np.array([[1,2],[3,4]])

#pass value into function
eg_val, eg_vect = linalg.eig(sample_array)

#get eigenvalues
print(“Eigen values”)
print(eg_val,”\n”)

#get eigenvectors
print(“Eigen Vectors”)
print(eg_vect)

Screenshots
find Eigenvalues and Eigen vectors of an array using scipy
List