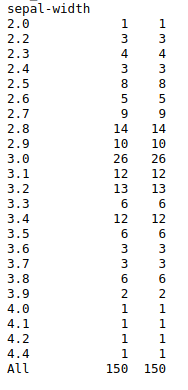
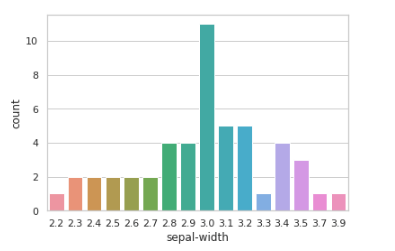
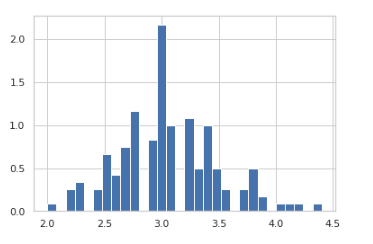
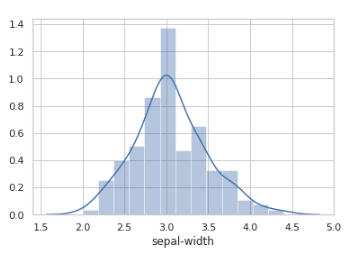
To find optimal number of clusters in k-means implementation in python.
Import necessary libraries and sub packages.
Read the data set.
Select the feature variables.
Declare the total number of clusters you want.
Initialize k-means cluster object.
Pass feature variable.
Calculate Silhouette score each number of clusters.
Print the optimal number of cluster
#import libraries
from sklearn import cluster
import sklearn
from sklearn import preprocessing
import matplotlib.pyplot as plt
data=pd.read_excel(‘/home/soft23/soft23/
Sathish/Pythonfiles/flyer.xlsx’)
#declare empty list to store silhouette_score
silhouette_score_values=list()
#select feature variable
X = data[[‘FlyingReturnsMiles’,’FlightTrans’]]
scaler = preprocessing.StandardScaler()
scaled_df = scaler.fit_transform(X)
print(“After scaling feature variable\n”,scaled_df)
#initialize how many cluster
NumberOfClusters=range(2,10)
#initialize for loop to calculate silhouette_score for each #cluster
for i in NumberOfClusters:
classifier=cluster.KMeans(i,init=’k-means++’, n_init=10, max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True)
classifier.fit(scaled_df)
labels= classifier.predict(scaled_df)
print (“Number Of Clusters:”)
print (i)
print (“Silhouette score value”)
print(sklearn.metrics.silhouette_score
(scaled_df,labels ,metric=’euclidean’, sample_size=
None, random_state=None))
silhouette_score_values.append
(sklearn.metrics.silhouette_score(scaled_df,labels ,
metric=’euclidean’, sample_size=None, random_state=None))
#plot the NumberOfClusters, silhouette_score_values
plt.plot(NumberOfClusters, silhouette_score_values)
plt.title(“Silhouette score values vs Numbers of Clusters “)
plt.show()
#find optimal number of clusters
Optimal_NumberOf_Components=
NumberOfClusters[silhouette_score_values.index
(max(silhouette_score_values))]
print (“Optimal number of clusters is:”,Optimal_NumberOf_Components)