Import necessary libraries.

   Load the sample data set.

   Assign the independent(X)and dependent(y) variables.

   Build the regression model.

   Make prediction.

#import libraries

import statsmodels.api as sm

import pandas as pd

#read the data set

data=pd.read_csv(‘/home/soft27/soft27

/Sathish/Pythonfiles/Employee.csv’)

#creating data frame

df=pd.DataFrame(data)

print(df)

#assigning the independent variable

X = df[[‘rating’,’bonus’]]

#assigning the dependent variable

Y = df[‘salary’]

#Build multiple linear regression

X = sm.add_constant(X)

#fit the variables in to the linear model

model = sm.OLS(Y, X).fit()

#print the intercept and regression co-efficients

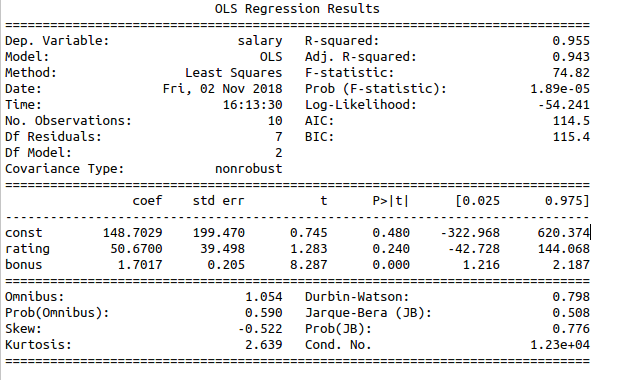
print_model = model.summary()

print(print_model)

#make predictions

predictions = model.predict(X)

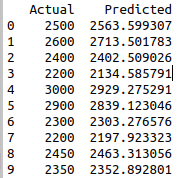
df1=pd.DataFrame({‘Actual’: Y, ‘Predicted’: predictions})

print(df1)