Import necessary libraries.

   Load the sample data set.

   Assign the independent(X)and dependent(y) variables.

   Train our data set in 70:30 manner.

   Pass the X_train and Y_train in to the linear model.

   Predict Y according to X.

#import the libraries

import pandas as pd

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

#Sample data set

data={‘age’:[25,26,25,23,30,29,23,24,26,25],

‘rating’:[4,3.6,2.5,2.25,4.5,4.4,3.9,3.5,3.7,3.2],

‘bonus’:[1300,1400,1250,1100,1500,

1450,1150,1100,1250,1200],’salary’:[2500,

2600,2400,2200,3000,2900,2300,

2200,2450,2350],}

#create data frame

df=pd.DataFrame(data)

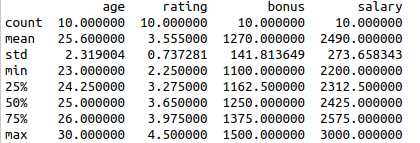
#Measuring descriptive statistics

print(df.describe())

#Take independent variable

X = df.iloc[:, :1].values

#Take dependent variable

y = df.iloc[:, 1].values

#Train our data

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=0)

#building linear model

regressor = LinearRegression()

#Fit the variable to the linear model

t=regressor.fit(X_train, y_train)

#print the linear model results

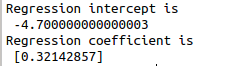
print(“Regression intercept is\n”,regressor.intercept_)

print(“Regression coefficient is\n”,regressor.coef_)

#make the predictions

y_pred = regressor.predict(X_test)

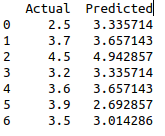
df1 = pd.DataFrame({‘Actual’: y_test, ‘Predicted’: y_pred})

#print the prediction as data frame

print(df1)