To implement LDA using python.
#import libraries
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
import warnings
warnings.filterwarnings(“ignore”)
#load data set URL
url = “https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data”
names = [‘sepal-length’, ‘sepal-width’, ‘petal-length’, ‘petal-width’, ‘class’]
data = pd.read_csv(url, names=names)
X = data.drop(‘class’,1)
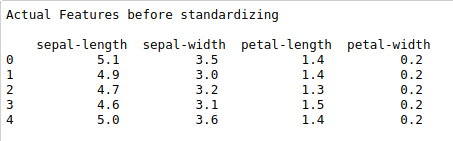
print(“Actual Features before standardizing\n\n”,X.head())
y = data[‘class’]
# Standardizing the features
X_trans = StandardScaler().fit_transform(X)
print(“\n”)
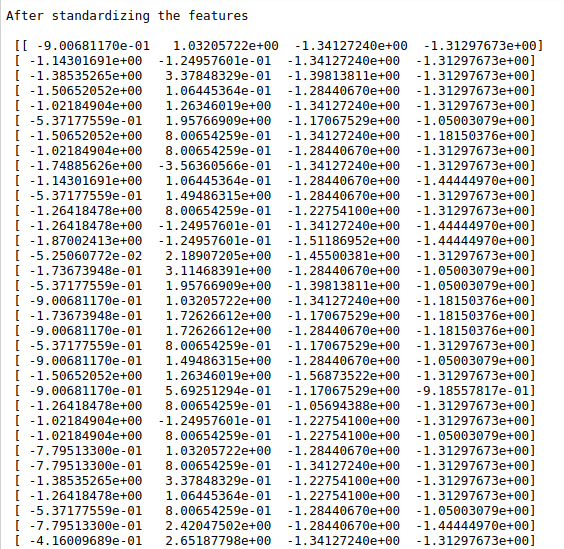
print(“After standardizing the features\n\n”,X_trans)
print(“\n”)
#covariance matrix
covar_matrix = LDA(n_components = 4)
covar_matrix.fit(X_trans,y)
variance = covar_matrix.explained_variance_ratio_
#Cumulative sum of variance
var=np.cumsum(np.round(variance, decimals=3)*100)
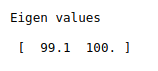
print(“Eigen values\n\n”,var)
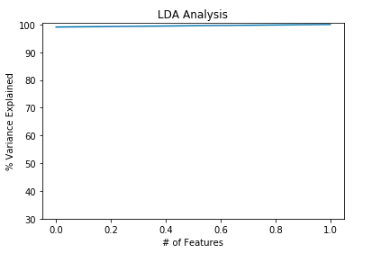
#plot for variance explained
plt.ylabel(‘% Variance Explained’)
plt.xlabel(‘# of Features’)
plt.title(‘LDA Analysis’)
plt.ylim(30,100.5)
plt.style.context(‘seaborn-whitegrid’)
plt.plot(var)
plt.show()
#Fit LDA for two components
lda = LDA(n_components = 2)
LinearComponents = lda.fit_transform(X_trans, y)
#make it as data frame
finalDf = pd.DataFrame(data = LinearComponents
, columns = [‘linear discriminant 1’, ‘linear discriminant 2’])
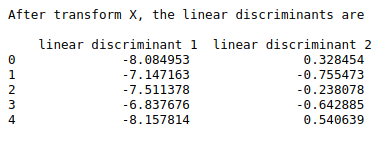
print(“After transform X, the linear discriminants are\n\n”,finalDf.head())
print(“\n”)
#data visualizations
print(“2D LDA Visualization\n”)
def visual(df):
np.random.seed(1)
sample_size = 5
df = df.sample(sample_size)
plt.figure(figsize=(8,5))
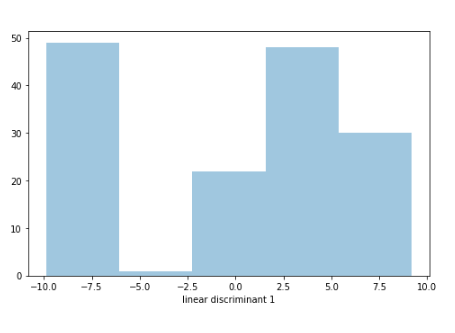
sns.distplot(finalDf[‘linear discriminant 1’], hist = True, kde = False,kde_kws = {‘linewidth’: 3})
plt.show()
visual(finalDf)
print(“\n”)
def visual1(df):
np.random.seed(1)
sample_size = 5
plt.figure(figsize=(8,5))
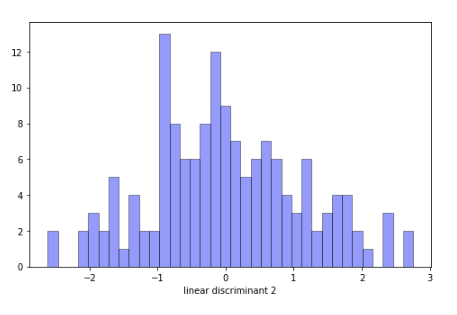
sns.distplot(finalDf[‘linear discriminant 2’], hist = True, kde=False,
bins=int(180/5), color = ‘blue’,
hist_kws={‘edgecolor’:’black’})
plt.show()
visual1(finalDf)
print(“\n”)
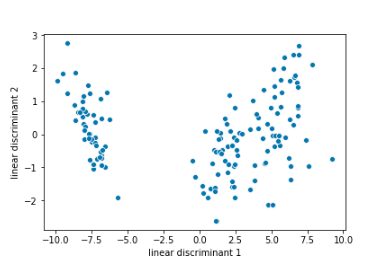
#scatter plot
ax = sns.scatterplot(x=”linear discriminant 1″, y=”linear discriminant 2″, data=finalDf)
plt.show()
print(“\n”)
print(“The explained variance percentage is:”,lda.explained_variance_ratio_*100)