Java Source for calculate Skewness and Kurtosis from a file

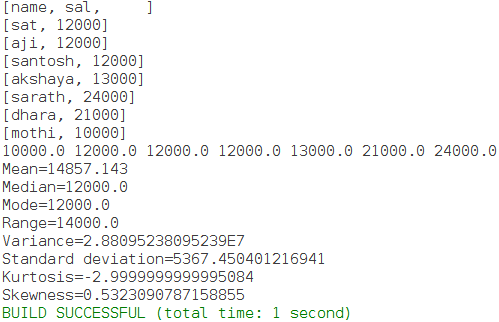
How to Calculate Skewness and Kurtosis from a File in Java?

Condition for Calculating Skewness and Kurtosis from a File in Java

Description: The Java code calculates skewness and kurtosis of a data set by first computing the mean and standard deviation. Skewness measures the asymmetry of the data distribution, while kurtosis evaluates the "tailedness" or peak of the distribution. These statistical measures help in understanding the shape and spread of the data, which is useful for data analysis.
To calculate skewness and kurtosis of a data set in Java, you first need to compute essential statistical measures like the mean and standard deviation. The mean gives the average value, which helps in understanding the central tendency of the data. The standard deviation measures the dispersion, indicating how spread out the data is around the mean.
Skewness is a measure of the asymmetry of the data distribution. A skewness value of 0 indicates a perfectly symmetrical distribution, while positive skewness suggests a distribution with a longer right tail, and negative skewness indicates a leftward tail.
Kurtosis, on the other hand, measures the "tailedness" of the distribution, showing whether data points are more or less concentrated around the mean compared to a normal distribution. Positive kurtosis indicates a sharp peak with heavy tails, while negative kurtosis suggests a flatter distribution with lighter tails.
The provided Java code reads a file containing numeric data, processes it, and calculates these statistical properties using their respective formulas. The results can then be used for further analysis, helping to identify patterns, outliers, and trends in the data. This approach is commonly applied in fields like data science, economics, and engineering for assessing data distributions.

Sample Source Code

# SkewnessKurtosis.java
package JavaSamples2;

import java.io.*;
import java.util.*;

public class SkewnessKurtosis {

public static void main(String[] args) {
String filePath = "data.txt";
List<Double> data = readDataFromFile(filePath);

if (data.isEmpty()) {
System.out.println("No data to process.");
return;
}

double mean = calculateMean(data);
double stdDev = calculateStandardDeviation(data, mean);
double skewness = calculateSkewness(data, mean, stdDev);
double kurtosis = calculateKurtosis(data, mean, stdDev);

System.out.println("Mean: " + mean);
System.out.println("Standard Deviation: " + stdDev);
System.out.println("Skewness: " + skewness);
System.out.println("Kurtosis: " + kurtosis);
}

public static List<Double> readDataFromFile(String filePath) {
List<Double> data = new ArrayList<>();
try (BufferedReader br = new BufferedReader(new FileReader(filePath))) {
String line;
while ((line = br.readLine()) != null) {
data.add(Double.parseDouble(line.trim()));
}
} catch (IOException e) {
System.out.println(e.getMessage());
}
return data;
}

public static double calculateMean(List<Double> data) {
double sum = 0;
for (double value : data) {
sum += value;
}
return sum / data.size();
}

public static double calculateStandardDeviation(List<Double> data, double mean) {
double sum = 0;
for (double value : data) {
sum += Math.pow(value - mean, 2);
}
return Math.sqrt(sum / data.size());
}

public static double calculateSkewness(List<Double> data, double mean, double stdDev) {
double sum = 0;
for (double value : data) {
sum += Math.pow((value - mean) / stdDev, 3);
}
return (data.size() / (double)((data.size() - 1) * (data.size() - 2))) * sum;
}

public static double calculateKurtosis(List<Double> data, double mean, double stdDev) {
double sum = 0;
for (double value : data) {
sum += Math.pow((value - mean) / stdDev, 4);
}
return ((data.size() * (data.size() + 1)) / (double)((data.size() - 1) * (data.size() - 2) * (data.size() - 3))) * sum - (3 * Math.pow(data.size() - 1, 2)) / ((data.size() - 2) * (data.size() - 3));
}
}

Screenshots

Data.txt File:

Step 1: The mean, standard deviation, skewness, and kurtosis are calculated and displayed.

List

Office Address

Social List

How to Calculate Skewness and Kurtosis from a File in Java?

Condition for Calculating Skewness and Kurtosis from a File in Java

Sample Source Code

Screenshots

Related Links

S-Logix (OPC) Private Limited